资源说明:
[](https://travis-ci.org/mattjj/pyhsmm)
# Bayesian inference in HSMMs and HMMs #
This is a Python library for approximate unsupervised inference in
Bayesian Hidden Markov Models (HMMs) and explicit-duration Hidden semi-Markov
Models (HSMMs), focusing on the Bayesian Nonparametric extensions, the HDP-HMM
and HDP-HSMM, mostly with weak-limit approximations.
There are also some extensions:
* [autoregressive models](https://github.com/mattjj/pyhsmm-autoregressive)
* [switching linear dynamical systems](https://github.com/mattjj/pyhsmm-slds)
* [factorial models](https://github.com/mattjj/pyhsmm-factorial)
## Installing from PyPI ##
Give this a shot:
```bash
pip install pyhsmm
```
You may need to install a compiler with `-std=c++11` support, like gcc-4.7 or higher.
To install manually from the git repo, you'll need `cython`. Then try this:
```bash
python setup.py install
```
It might also help to look at the [travis file](https://raw.githubusercontent.com/mattjj/pyhsmm/master/.travis.yml) to
see how to set up a working install from scratch.
## Running ##
See the examples directory.
For the Python interpreter to be able to import pyhsmm, you'll need it on your
Python path. Since the current working directory is usually included in the
Python path, you can probably run the examples from the same directory in which
you run the git clone with commands like `python pyhsmm/examples/hsmm.py`. You
might also want to add pyhsmm to your global Python path (e.g. by copying it to
your site-packages directory).
## A Simple Demonstration ##
Here's how to draw from the HDP-HSMM posterior over HSMMs given a sequence of
observations. (The same example, along with the code to generate the synthetic
data loaded in this example, can be found in `examples/basic.py`.)
Let's say we have some 2D data in a data.txt file:
```bash
$ head -5 data.txt
-3.711962552600095444e-02 1.456401745267922598e-01
7.553818775915704942e-02 2.457422192223903679e-01
-2.465977987699214502e+00 5.537627981813508793e-01
-7.031638516485749779e-01 1.536468304146855757e-01
-9.224669847039665971e-01 3.680035337673161489e-01
```
In Python, we can plot the data in a 2D plot, collapsing out the time dimension:
```python
import numpy as np
from matplotlib import pyplot as plt
data = np.loadtxt('data.txt')
plt.plot(data[:,0],data[:,1],'kx')
```
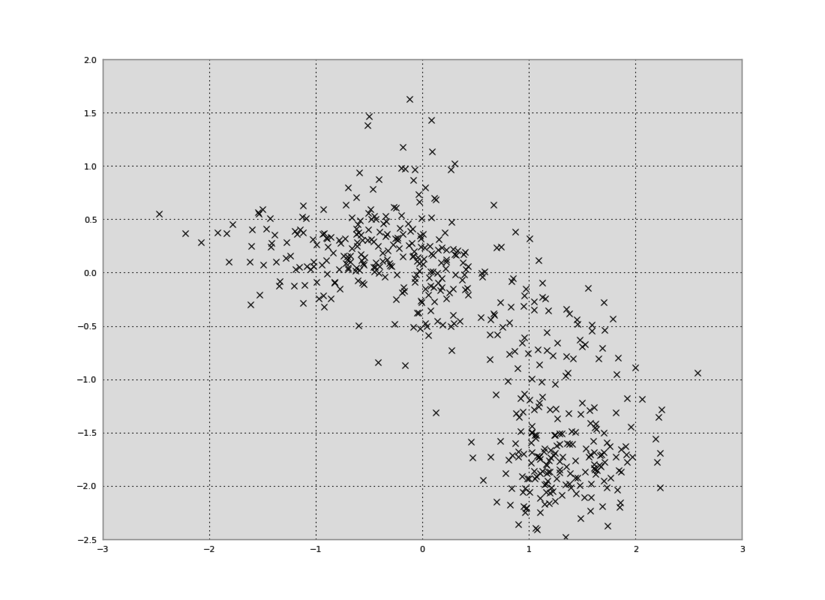
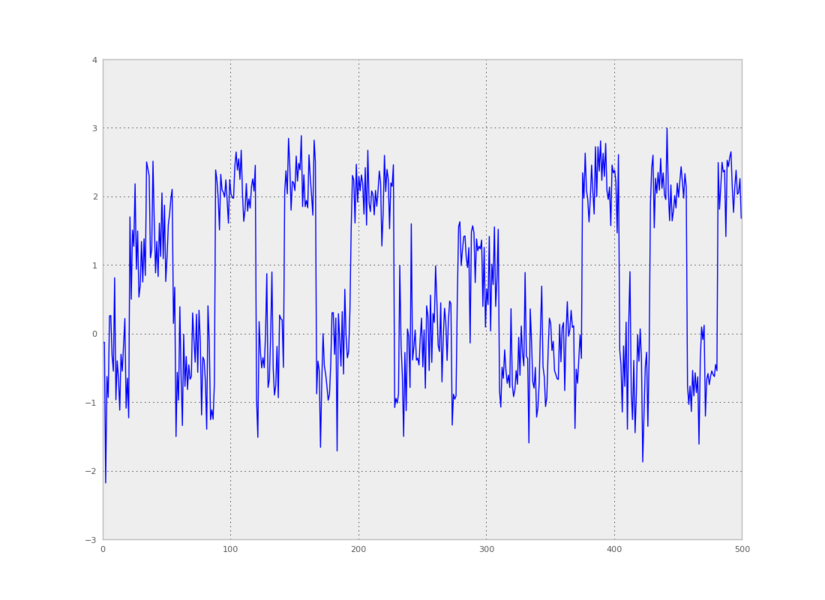
We can also make a plot of time versus the first principal component:
```python
from pyhsmm.util.plot import pca_project_data
plt.plot(pca_project_data(data,1))
```
To learn an HSMM, we'll use `pyhsmm` to create a `WeakLimitHDPHSMM` instance
using some reasonable hyperparameters. We'll ask this model to infer the number
of states as well, so we'll give it an `Nmax` parameter:
```python
import pyhsmm
import pyhsmm.basic.distributions as distributions
obs_dim = 2
Nmax = 25
obs_hypparams = {'mu_0':np.zeros(obs_dim),
'sigma_0':np.eye(obs_dim),
'kappa_0':0.3,
'nu_0':obs_dim+5}
dur_hypparams = {'alpha_0':2*30,
'beta_0':2}
obs_distns = [distributions.Gaussian(**obs_hypparams) for state in range(Nmax)]
dur_distns = [distributions.PoissonDuration(**dur_hypparams) for state in range(Nmax)]
posteriormodel = pyhsmm.models.WeakLimitHDPHSMM(
alpha=6.,gamma=6., # better to sample over these; see concentration-resampling.py
init_state_concentration=6., # pretty inconsequential
obs_distns=obs_distns,
dur_distns=dur_distns)
```
(The first two arguments set the "new-table" proportionality constant for the
meta-Chinese Restaurant Process and the other CRPs, respectively, in the HDP
prior on transition matrices. For this example, they really don't matter at
all, but on real data it's much better to infer these parameters, as in
`examples/concentration_resampling.py`.)
Then, we add the data we want to condition on:
```python
posteriormodel.add_data(data,trunc=60)
```
The `trunc` parameter is an optional argument that can speed up inference: it
sets a truncation limit on the maximum duration for any state. If you don't
pass in the `trunc` argument, no truncation is used and all possible state
duration lengths are considered. (pyhsmm has fancier ways to speed up message
passing over durations, but they aren't documented.)
If we had multiple observation sequences to learn from, we could add them to the
model just by calling `add_data()` for each observation sequence.
Now we run a resampling loop. For each iteration of the loop, all the latent
variables of the model will be resampled by Gibbs sampling steps, including the
transition matrix, the observation means and covariances, the duration
parameters, and the hidden state sequence. We'll also copy some samples so that
we can plot them.
```python
models = []
for idx in progprint_xrange(150):
posteriormodel.resample_model()
if (idx+1) % 10 == 0:
models.append(copy.deepcopy(posteriormodel))
```
Now we can plot our saved samples:
```python
fig = plt.figure()
for idx, model in enumerate(models):
plt.clf()
model.plot()
plt.gcf().suptitle('HDP-HSMM sampled after %d iterations' % (10*(idx+1)))
plt.savefig('iter_%.3d.png' % (10*(idx+1)))
```
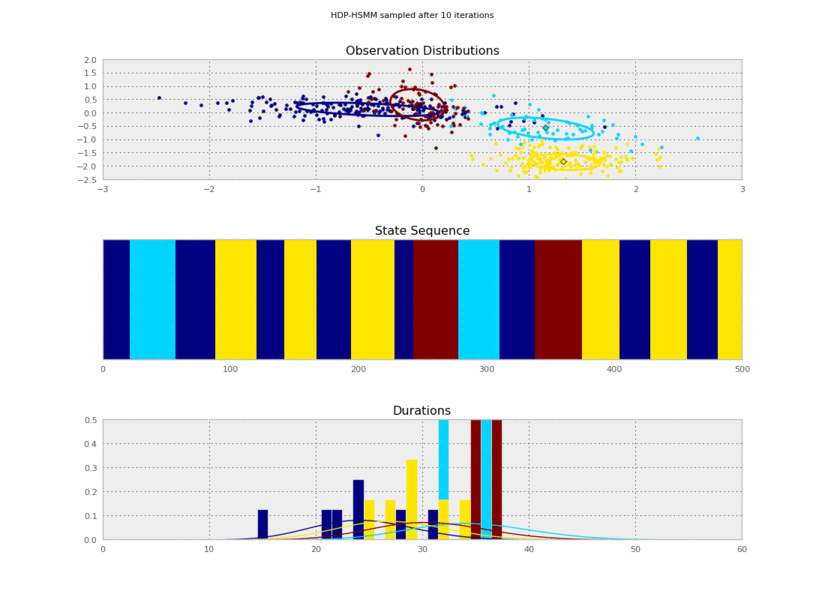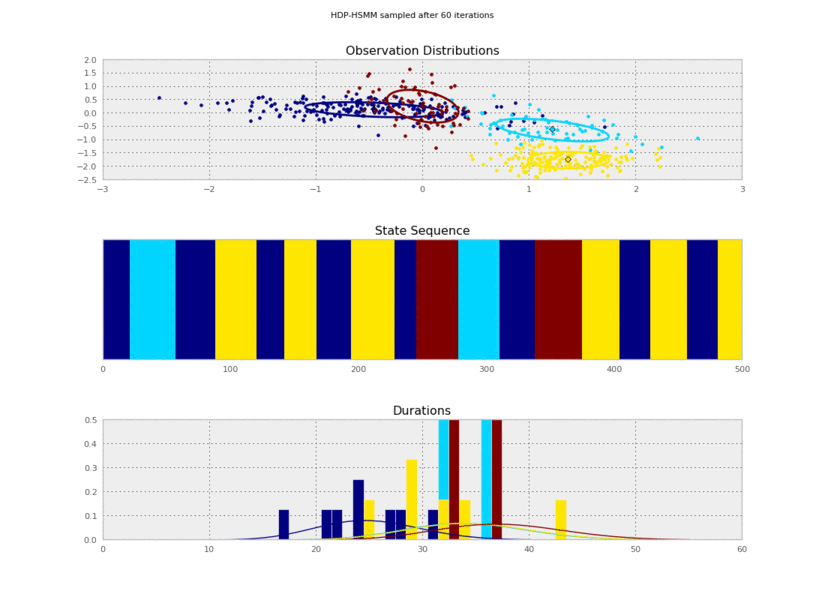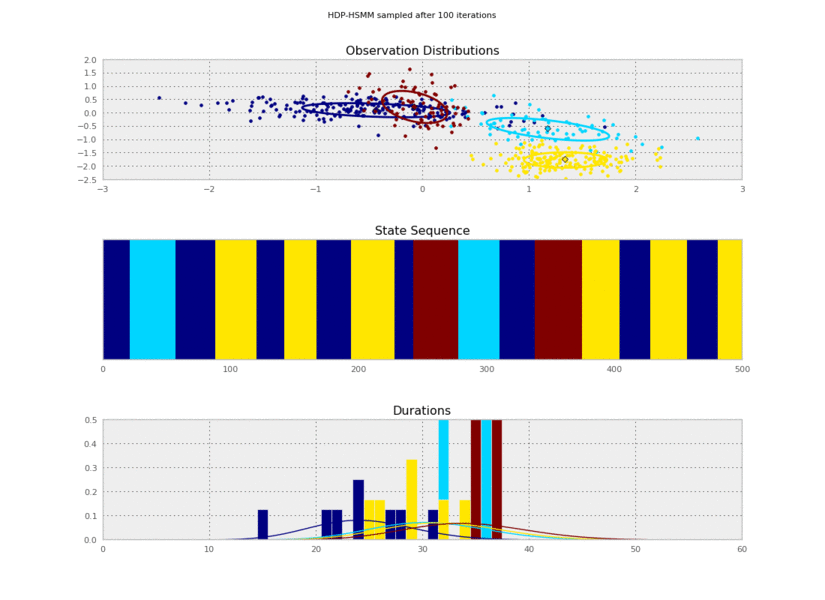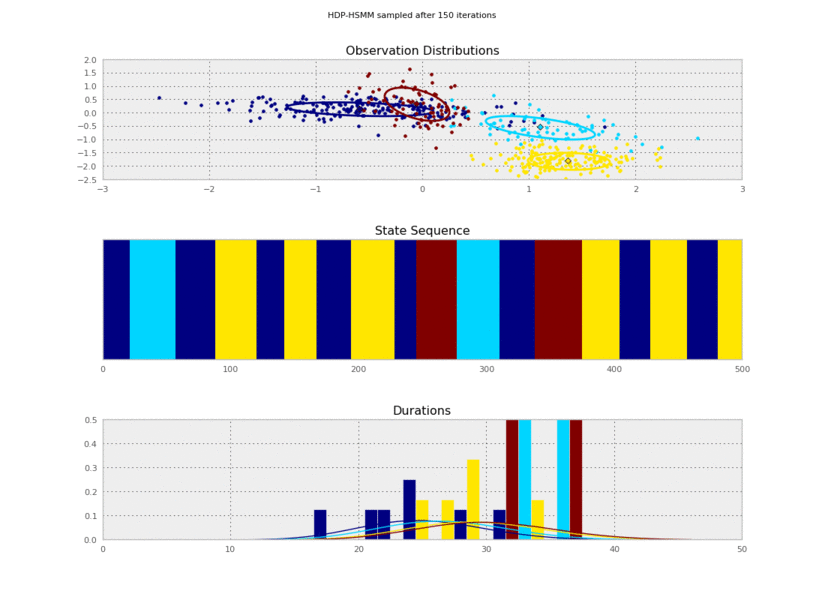
I generated these data from an HSMM that looked like this:
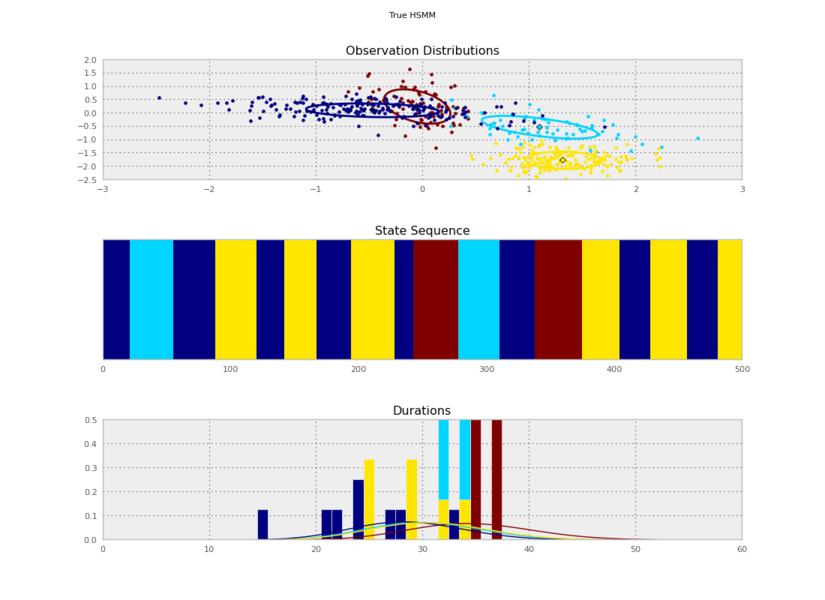
So the posterior samples look pretty good!
A convenient shortcut to build a list of sampled models is to write
```python
model_samples = [model.resample_and_copy() for itr in progprint_xrange(150)]
```
That will build a list of model objects (each of which can be inspected,
plotted, pickled, etc, independently) in a way that won't duplicate data that
isn't changed (like the observations or hyperparameter arrays) so that memory
usage is minimized. It also minimizes file size if you save samples like
```python
import cPickle
with open('sampled_models.pickle','w') as outfile:
cPickle.dump(model_samples,outfile,protocol=-1)
```
## Extending the Code ##
To add your own observation or duration distributions, implement the interfaces
defined in `basic/abstractions.py`. To get a flavor of
the style, see [pybasicbayes](https://github.com/mattjj/pybasicbayes).
## References ##
* Matthew J. Johnson. [Bayesian Time Series Models and Scalable
Inference](http://www.mit.edu/~mattjj/thesis.pdf). MIT PhD Thesis, May 2014.
* Matthew J. Johnson and Alan S. Willsky. [Bayesian Nonparametric Hidden
Semi-Markov Models](http://www.jmlr.org/papers/volume14/johnson13a/johnson13a.pdf).
Journal of Machine Learning Research (JMLR), 14:673–701, February 2013.
* Matthew J. Johnson and Alan S. Willsky, [The Hierarchical Dirichlet Process
Hidden Semi-Markov Model](http://www.mit.edu/~mattjj/papers/uai2010.pdf). 26th
Conference on Uncertainty in Artificial Intelligence (UAI 2010), Avalon,
California, July 2010.
```bibtex
@article{johnson2013hdphsmm,
title={Bayesian Nonparametric Hidden Semi-Markov Models},
author={Johnson, Matthew J. and Willsky, Alan S.},
journal={Journal of Machine Learning Research},
pages={673--701},
volume={14},
month={February},
year={2013},
}
```
## Authors ##
[Matt Johnson](https://github.com/mattjj), [Alex Wiltschko](https://github.com/alexbw), [Yarden Katz](https://github.com/yarden), [Chia-ying (Jackie) Lee](https://github.com/jacquelineCelia), [Scott Linderman](https://github.com/slinderman), [Kevin Squire](https://github.com/kmsquire), [Nick Foti](https://github.com/nfoti).
本源码包内暂不包含可直接显示的源代码文件,请下载源码包。
 English
English
